基于时间序列聚类的可转债投资组合分析
本文是一篇投资分析论文,本文提出的基于两阶段聚类的可转债投资组合,主要是将转债拆分为正股价格决定的平价以及市场预期等因素决定的溢价两部分,分别通过结构特征和曲线整体形态进行两阶段聚类,再将可转债的两阶段聚类结果用于最大夏普比率投资组合中减少搜索空间并在一定程度上更好地分散风险。
1.绪论
1.1 研究背景与意义
1.1.1 研究背景
可转债属于一种特殊的金融衍生证券,其兼具股权性、债权性以及可转换期权三大属性。可转债的特殊条款对投资者及发行者都会产生很大影响,我国可转换债券行业中发行的可转换债券通常涵盖三种主要附加条款,具体包括转股价下修、赎回以及回售条款。第一,转股价格向下修正条款是指当转债正股价格达成一定条件后公司可以下调自己的转股价。举例来说,一种典型的转债下修条款规定如下:在任何连续30个交易日内,如果有15个交易日的股价低于当时转股价的90%,公司董事会就有权将转股价格下调。第二,赎回条款是指可转换债券的发行方在特定条件下可按约定价格向投资者赎回债券。举例来说,一种常见的赎回条款规定如下:在转股期间,如果连续30个交易日中有15个交易日,可转债的正股价格未达到转股价的130%,则公司有权以债券面值加上当期应计利息的方式,全部或部分未转股的可转债进行赎回。第三,回售条款是指在转债正股价格下跌到一定程度时,可转债持有人有权按约定价格将转债卖回给发行人的权利。举例来说,一种常见的回售条款设定为:在转债的末期的2个计息年度,若公司股票价格在任意30天的收盘价不到当时转股价的 70% 以下,则可转债持有人有权以票面价值加当期应计利息的方式,将所持有的可转债的所有或部分卖回给公司。
对于投资者而言,可以依据转债条款在一定条件下按一定比率将可转债转化为发行人对应的普通股股票(发行人对应的股票称为正股),既能够享有债券的利息收益,又能够选择转化为正股,享有正股的资本增值和股息收益。类似于传统的企业债券,可转债的发行条款中明确规定了各年度的债券利率、利息支付时间和最终回售时间。若投资者持有可转债直到最终回售时间,那么可转债就相当于利率较低的普通企业债,投资者可获得利息收入。目前大部分可转债的票面利率在1% 左右,而一般情况下信用评级是AA-的企业债的利率可能高于 7% ,单纯从债权的角度来看,可转债相较于普通企业债没有优势。然而,可转债中附加的转股期权为投资者在债权收益外附加了期权价值收益。投资者可在转股期内寻找正股发展符合预期、公司市值增长的时点进行转股操作,享有企业发展带来的增值收益。同时,依托于债权特性,可转债是一种更加稳健的金融衍生品。当对应正股价格下行时,转债产品由于具有纯债价值的底价保护,其价格波动通常小于对应的正股,呈现抗跌性;当对应正股价格上行时,转债产品由于转股期权的存在,可以享受正股带来的超额回报。
.......................
1.2 研究现状
由于目前对于可转债的研究绝大多数从发行者角度出发,研究可转债的定价问题以及可转债的融资效应,缺乏从投资者角度出发指导可转债投资组合的研究。为了从已有研究中寻找研究思路,需从可转债的定价和可转债的融资效应出发探索可转债的特点,并梳理投资组合的研究,最后结合可转债时序特点梳理时间序列聚类的相关研究。 1.2.1 可转债研究现状
目前对于可转债的研究绝大多数从发行者角度出发,研究可转债的定价问题以及可转债的融资效应。为了加深对于可转债产品的认识,本节将从可转债的定价问题和可转债的融资效应两个方面出发梳理相关研究。
其一,可转债的定价问题。作为一种内嵌多元条款期权的复杂衍生品,可转债的价值估算问题具有较大难度。由于可转债的内在条款越来越繁杂,而且各种条款之间的相互影响也越来越大,这就给可转债的定价带来了更大的困难。因此,许多学者为可转债的定价问题贡献了不少研究方法。从本质上讲,可转换债券的定价方法可以分为两大类:一是解析式方法,二是数值型方法。
其二,可转债的融资效应。可转换债券作为一种主要的再融资方式,其发行过程在实际中会给企业带来巨大的财富波动,同时也会对市场造成不可忽视的冲击。所以,关于可转换债券的融资效果的国内外研究很多,大致可以划分为两个方面:一是可转换债券对公司股票价格的公告效应,二是可转换债券对企业绩效能力的影响。
.........................
2.相关理论基础
2.1 时间序列的经验模态分解去噪
金融时间序列通常具有噪音特征,在实际场景下投资组合的回报空间对噪音十分敏感。如果忽视噪音不仅会导致研究结果失真,也会导致投资者难以获得高效、鲁棒的投资策略。经验模式分解(Empirical Mode Decomposition,EMD)是一种对非线性、非平稳时序数据具有极强的自适应能力的方法,利用 EMD 对金融时序数据进行去噪广泛适用于金融业务场景。
2.1.1 经验模态分解
原始数据被 EMD 方法分解成一组本征模态函数(IMFs)。能够成为 IMFs 要求其满足如下两个条件:(1)全时序上的极值数与零交点必须相等,或者最多有一个差值。(2)由局部极小值与局部极大值确定的包络面平均在任一点上取值为零。进一步可以将时间序列????(????),????=1,2,⋯,????分解为 IMF 和残差之和,如式2.1所示:

投资分析论文怎么写
...........................
2.2 时间序列的相似性度量
本节将对于时间序列间的相似性度量进行介绍,有基于距离的度量 DTW 距离和 SBD 距离,也有基于局部结构的 U-shapelets 提取方法。
2.2.1 DTW距离
一方面,在真实的时间序列应用场景中,由于存在离群点、数据缺失以及数据的动态性等因素,使得不同的时间序列具有不同的长度。同时,由于时序的关联性特征,各时序节点之间存在着一定的相关性。从而导致传统的相似性测度如欧式距离与相关系数失效。另一方面,曲线整体波动形态的相似性并不必然在时间轴上完全相同,允许存在滞后效应或领先效应,但是需要保证整体波动态势的相似度。因此,传统的相似性测度在此场景下也会失效。一种直观的方法是对时序数据进行时间尺度的扩展收缩,使得两个时序之间的匹配性更高,从而产生了“动态时间扭曲”的思想。
DTW 采用动态规划方法,从距离矩阵中找到最短路径,从而有效处理时间漂移问题。
2.2.2 SBD 距离
SBD 距离的产生基于互相关测度,而互相关是一种统计度量,其在信号处理领域中常被用来处理信号序列中存在的振幅和相位畸变,因此我们可以用它来确定两个长度为 m 的序列之间的相似性。假定有 ????={????1,????2,⋯,????????}、????={????1,????2,⋯,????????}这两个时间序列。在滑动不变的目的下,进行互相关分析时必须使 Y 处于静止状态。
..............................
3.基于可转债两阶段聚类的投资组合 .............................. 29
3.1 基于经验模态分解的转股溢价率去噪 .......................... 29
3.2 基于可转债转股溢价率结构特征的初步聚类 ................... 31
4.实验分析 .......................................... 44
4.1 回测时段选择 ................................... 44
4.2 可转债的两阶段聚类 ............................ 46
5.总结展望 ................................. 62
5.1 总结 .................................. 62
5.2 展望 ......................... 64
4.实验分析
4.1 回测时段选择
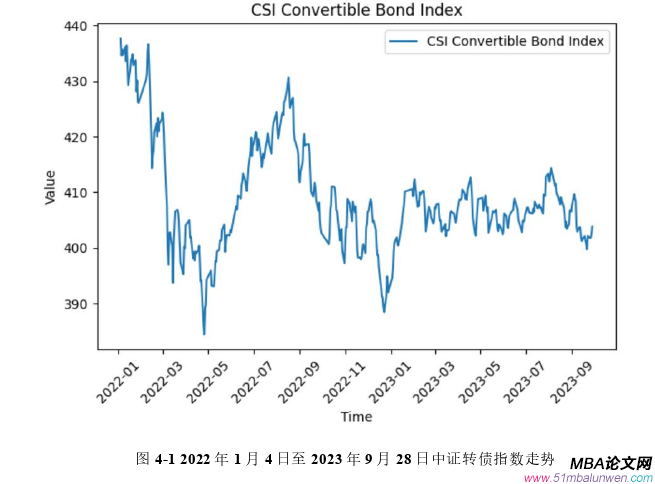
在不同的市场周期下可转债的表现具有一定的灵活性和多样性,如何选择合适的市场周期进行回测可以帮助投资者更好地理解和评估可转债投资组合在不同市场环境下的表现,也能够全面展现出所提出的方法的优劣。可以大致将市场周期分为牛市、熊市和震荡市三种类型。其一,在牛市中股市通常处于上涨趋势,并且投资者情绪乐观,股票价格上涨。对于可转债而言,牛市通常意味着股票价格的上涨,因此转股价值可能增加,从而提升了可转债的吸引力。在牛市中,可转债通常表现出更多的股票属性,投资者可能更愿意持有,因为有机会获得股票市场上涨的红利。其二,在熊市中股市下跌,并且投资者情绪悲观。在这种市场环境下,可转债的债券属性更加突出,因为它们通常有固定的债券利息和到期赎回价值。投资者可能更倾向于看好其债券部分,以稳定投资组合价值。其三,在震荡市中股票价格可能上下波动,没有明显的主导趋势。在这种市场环境下,可转债通常会展现其多元化的特性,即债券和股票的特性都有可能对其表现产生影响。投资者可能更加注重选择具有良好风险调整收益的可转债,以便在市场波动中保持较稳定的投资回报。因此,选择的回测时段需要同时考虑到牛市、熊市和震荡市,以便全面展现出所提出的可转债投资组合在不同市场环境下的表现。
投资分析论文参考
.......................
5.总结展望
5.1 总结
对于可转债的投资组合问题,一个好的投资组合构建应当保证充分考虑可转债的债性、股性以及赎回、回售和下修等特殊条款的影响,并将具有相同波动性质的可转债进行分散投资。本文提出的基于两阶段聚类的可转债投资组合,主要是将转债拆分为正股价格决定的平价以及市场预期等因素决定的溢价两部分,分别通过结构特征和曲线整体形态进行两阶段聚类,再将可转债的两阶段聚类结果用于最大夏普比率投资组合中减少搜索空间并在一定程度上更好地分散风险,具体如下:
(1)研究了如何对由市场预期等因素决定的转股溢价率进行聚类。本文将含噪的转股溢价率序列通过基于相关系数的经验模态分解进行去噪,首先从转股溢价率的全局形态出发,抽取了均值、中位数、标准差、极差、偏度、峰度和样本熵这七个全局统计特征。考虑到可转债转股溢价率的波动性极高,单靠全局性统计特征难以全面描述其形态波动特点。因此,我们探索采用基于U-shapelets的方法,从转股溢价率曲线中提取出代表性的结构信息。但是原有 U-shapelets 提取的 BF 算法存在三方面不足:一是备选 shapelets 过多,计算复杂度过大;二是计算 shapelets 与序列间的距离依赖滑动窗口的方式。进一步加大了计算的复杂度;三是判别 shapelets 优劣的 gap 值逻辑性不强。第一,为了解决备选 shapelets 过多的问题,本文提出了一种 shapelets 备选方法,该方法首先抓取时间序列中的极值点,并对极值点进行筛选剔除干扰点, 同时定义两个候选点间所夹的曲线满足备选 shapelets 的要求。第二,为了解决原始算法中计算 shapelets 与序列间的距离通过滑动窗口的方式计算欧氏距离,本文从互相关测度出发,采用 SBD 距离计算 shapelets 与序列间的距离。由于 SBD 距离可以采用傅里叶变化进行加速,可以提高 shapelets 与序列间距离的计算效率。第三,为了解决判别 shapelets 优劣的 gap 值逻辑性不强的问题,可以依据线性判别分析的思路构造一个新的gap 值。可以将 shapelets 与序列间的距离理解为每个序列映射到 shapelets 维度后的特征,那么如果这个特征能将序列较好区分开便成为了优质的 shapelets ,所谓的将序列区分开可以进一步拆解为依据这个特征以及某个阈值将序列分为两类后,类内特征的紧密度高,类间特征的紧密度低。最后,抽取了五个最优 shapelets ,得到了序列与这五个 shapelets 间的距离矩阵 D,距离矩阵 D 即为时间序列投影到最优 shapelets 空间的特征。并基于这十二个形态特征,采用 K-means++ 算法对可转债转股溢价率的时序集合进行初步聚类。在实证分析中,基于这十二个形态特征采用 K-means++ 算法对可转债转股溢价率的时序集合进行初步聚类,选择 SSE 曲线拐点处对应的 K 值,确定区间一、区间二和区间三内第一层聚类的类别数为 3 。
参考文献(略)


