卫星位姿模拟平台几何误差检测及补偿方法的探讨
本文是一篇决策模拟论文,论文以卫星位姿模拟平台为研究对象,探讨了该平台中几何误差对综合定位精度的影响,为了降低该影响从而减小空间综合误差,以误差补偿为最终目标展开了研究。
1 绪论
1.1课题背景及研究意义
卫星技术在近代已经在各领域中成为一种新型的技术手段,其技术也赋能了各行各业的高质量发展,在一定程度上促进着我国社会的发展,逐渐成为我国经济发展和民生服务的重要支柱。在全球范围内,我国的遥感卫星技术已居先进水平,对于遥感卫星的应用也迈进了新阶段[1]。 在卫星的各项应用工作中,卫星的空间位置及姿态的准确获取是影响卫星高精度工作的重要基础[2][3][4]。
为了实现空间中卫星位置及姿态的精准定位[5],需先先建立其在地面上的模拟系统[6]。六自由度运动平台凭借其良好的动态性能,可以方便完成在各方向的运动工作[7],可灵活地模拟卫星在空间中的任意时刻的位置和姿态,同时,它也是整个模拟系统中实行位姿捕捉工作的关键子系统,所以,单台卫星模拟平台末端执行工作的准确度直接影响到卫星位姿坐标数据的精准性。
在单台模拟平台中,误差来源具有多样性,其中主要包括平台的几何误差、热误差、载荷误差以及运动的控制误差等关键因素。这些误差源共同影响着平台的性能[8]。其中几何误差主要源自设计、制造及装配阶段的不足,这些不足导致部件实际与理想的几何参数或位置出现偏差。另外,系统的热误差主要是在系统关键的执行部件在运动过程中产生,例如导轨运动产生摩擦从而引发热变形;载荷误差出现的原因主要在实际应用过程中,系统因装夹力、载台载物的重力等因素引起的变形,系统载荷误差的形成往往和系统自身的刚性有关;而控制误差产生的主要原因是系统伺服参数的不匹配或者对运动的控制不当等,从而导致平台运动不同步而产生的误差。
...................................
1.2国内外研究现状
1.2.1几何误差元素分析
机械结构的几何误差按照与系统运动状态的关系可以分为两大类:位置无关几何误差(PIGES)和位置有关几何误差(PDGES)。其中位置无关几何误差主要是因为机构在最初生产的过程中因其零部件装配不当所导致,具体地可以理解为零部件在装配过程中因为施加了载荷或者温度变化等因素而引起的装配误差。因为这类误差在生产及安装过程中便产生便客观存在,所以它不会随着系统运动部件的运动发生变化而跟着变化,因此被称为位置无关。例如,当一个机械系统完成安装工作,安装完成后系统的各轴线的倾斜误差就是与系统整体的运动状态无关的位置无关误差,因此也被归类为系统的结构误差,因为这些误差与机械结构本身的状态和配置紧密相关,而非受到操作位置或工作状态的影响[9];而位置有关几何误差的产生源头是系统内部的各部件在最初的生产过程中其自身表面的精度不足问题,在系统整体的运动过程中该问题就表现为各位置处的位置误差或者形状误差,这类与系统末端所处位置有关的误差就被称为运动误差,因为它们会随着零部件的运动状态的变化而发生变化[10]。
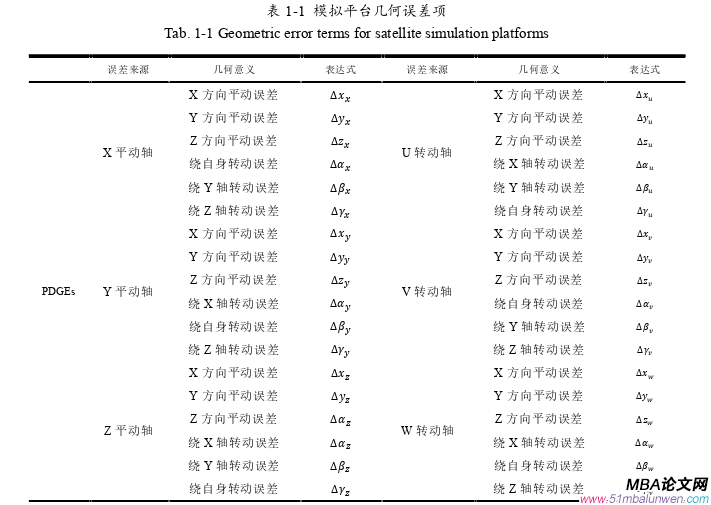
ISO230-1[11]中指出,在多自由度机械系统中,系统整体的综合运动是靠各运动部件的相互配合完成的,而各运动部件在独立运动过程中,均会产生相关几何误差。例如,平动轴在平移过程中就可能会产生6项几何误差,分别为3项位置误差以及3项角度误差,除此之外,三个平动轴之间也存在着两两之间的垂直度误差,共3项,所以六自由度的卫星位姿模拟平台中三个平动轴上的总误差共计21项;旋转轴在转动过程中也可能会产生6项几何误差,分别为3项位置误差和3项角度误差,另外,每个旋转轴还伴随着4项结构误差,分别是2项位置误差和2项垂直度误差,所以,三个旋转轴的总误差项为30项,加上平动轴的21项误差,该平台总计共有51项几何误差。对误差项的整理及具体各误差项的含义如表1-1所示。
决策模拟论文怎么写
.........................................
2 卫星位姿模拟平台综合误差建模及误差元素灵敏度分析
2.2 卫星位姿模拟平台运动结构及其几何误差元素分析
2.2.1 六自由度卫星位姿模拟平台结构
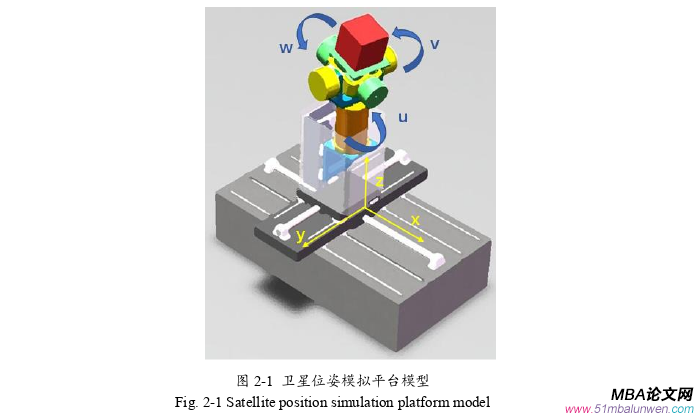
因为卫星模拟平台需要模拟卫星在空间中任意时刻的任意位置及姿态,且使用中要求六个方向的运动需各具独立速度及独立加速度、六轴具有空间联动功能,所以,卫星位姿的模拟平台设计为正交加三串联的六自由度运动机构,基于Solidworks设计的模拟平台如下图2-1所示。
决策模拟论文参考
模拟平台的几何误差主要产生于系统的制造和装配过程中,其主要体现在各个运动轴的轴线与理想轴线之间的偏差、各运动轴的定位误差等,而这些误差在各运动轴上导致的各轴运动精度则会直接或间接地影响模拟平台整体的定位精度。关于制造和装配过程中产生的几何误差,又通常分为两类:位置相关的几何误差(PDGEs)和位置无关的几何误差(PIGEs)。
...................
2.3卫星位姿模拟平台综合误差模型的建立
模拟平台的运动系统可以看成是刚体运动系统,如果可以将模拟平台的每一个运动轴都看作独立的刚体的话,便可以为其每个独立刚体都设立专门的坐标系,从而可以用齐次坐标来表达刚体间的运动传递关系。在一般的笛卡尔坐标系中,刚体的运动包含3种平移及3种旋转。刚体整体上的综合运动也是通过这6个刚体的协同配合来实现,可以将模拟平台上各轴的运动看成是刚体的相对运动,把几何误差看作是各轴上的微小的位移或转动,基于此,就可以构建平台的运动传递模型。
位姿模拟平台的系统空间误差模型详尽地描述了平台各运动轴之间的位置和运动关系,它不仅包含了各误差元素对位姿的具体影响,还揭示了这些误差元素之间的内在关联。这一模型为平台几何误差的补偿提供了理论依据。位姿模拟平台的系统空间误差模型能够同时集成各运动部件的位姿、运动和误差信息,但这种集成性也导致了模型结构的复杂性,给模型分析带来了显著挑战,同时也增加了在实际应用中的操作难度。因此,通过灵敏度分析来识别对平台误差影响显著的关键几何误差元素,可以有效简化误差模型中的信息量,保留关键有效信息,提高模型实际应用效率。
.................................
3 基于激光跟踪仪多站的模拟平台几何误差的检测 .......................... 21
3.1 引言 ............................... 21
3.2 激光跟踪仪多站检测原理及站位坐标自标定 ............................ 21
4 卫星位姿模拟平台几何误差的识别 .................................. 29
4.1 引言 ........................................ 29
4.2 平动轴相关误差项识别................................. 29
5 卫星位姿模拟平台几何误差补偿实验分析 ..................... 47
5.1 引言 .................................................... 47
5.2 几何误差补偿方法概述............................. 47
5 卫星位姿模拟平台几何误差补偿实验分析
5.2 几何误差补偿方法概述
对多自由度机构中的误差进行补偿是一个长期且不断发展的领域。根据其发展历程,补偿技术主要可以分为以下三种:
5.2.1 机械式静态补偿法
机械式(硬件)的静态补偿法很长一段时间在机械结构误差的修正领域都占据着主导地位。近几十年来,该方法也随着技术的进步和需求的增加应用在更多方面。在进行静态补偿时,经常用到的方法有:调整读数设备的读数示值、修正传动部件的位移等。这些方法虽然有效,但随着自动化和精密加工技术的发展,对误差补偿的精度和效率要求越来越高,因此,新的补偿技术也在不断被研究和应用。
机械式补偿作为一种固定补偿方法,其本质是将补偿数据或函数直接“嵌入”到硬件中。这种方法具有高度的可靠性,因为补偿参数是直接通过物理结构实现的。然而,一旦补偿规律被硬件化(例如,修正尺的轮廓或凸轮的形状被确定),其补偿量就变得难以调整。这意味着补偿只能按照预先设定的值进行,而无法根据实际的加工情况进行实时反馈控制。
决策模拟论文参考
............................
6 总结与展望
6.1 总结
论文以卫星位姿模拟平台为研究对象,探讨了该平台中几何误差对综合定位精度的影响,为了降低该影响从而减小空间综合误差,以误差补偿为最终目标展开了研究。研究主要工作有:
(1)针对不同类型的几何误差进行了详尽的分析和描述,基于刚体运动学,建立模拟平台的系统空间误差模型,为进一步明确各几何误差对定位精度的影响程度,开展了几何误差的灵敏度分析,解决了误差项灵敏度指标过多的问题,提高了检测效率。
(2)针对激光跟踪仪的多站检测精度进行了优化。着重分析了在多站分时测量中激光跟踪仪基站站位的分布对基站标定精度的影响。构建了基站布局优化函数,并据此提出了一种基于激光跟踪仪的基站布局方案。为现场测量实验中基站位置的分布提供了参考依据。
(3)设计了模拟平台空间误差检测方法与几何误差辨识方法。针对模拟平台几何误差的研究中,充分考虑不同误差项的特性,对不同类型的几何误差进行了合理的描述,将几何误差的辨识问题转化为多项式系数或空间几何量的辨识。对模拟平台的空间误差进行了检测,应用和验证了提出的几何误差辨识方法。
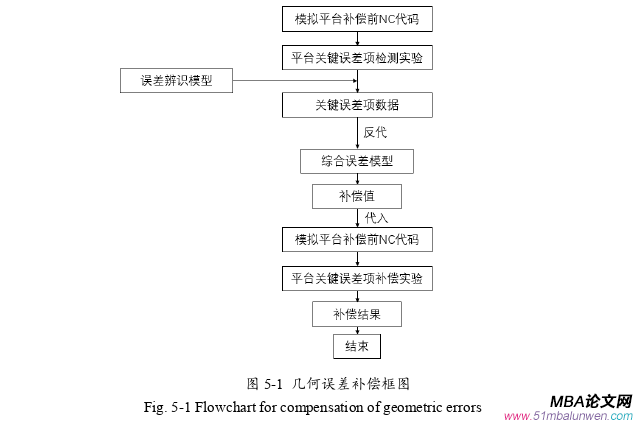
(4)应用本文研究成果,形成了模拟平台误差的补偿方案。利用提出的NC代码修改误差补偿方法,对平台几何误差进行软件补偿,将补偿前、后的NC代码载入平台数控系统,开展了误差补偿实验,最终使补偿后空间的位置最大误差从61.2 μm减小到12.3 μm,姿态最大误差从15.8 ″减小到6.7 ″,达到了卫星位姿模拟平台的设计要求,均方根误差在X、Y、Z、U、V、W方向依次分别减少了75.42%、58.2%、56.1%、62.2%、49.2%、50%,有效降低了系统误差的离散程度,使系统定位误差分布更加均衡。通过补偿的效果分析,证明了本文误差补偿方法的合理性。
参考文献(略)


